소수 정리
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
소수 정리는 소수의 분포에 대한 중요한 정리로, 임의의 실수 x에 대해 x보다 작거나 같은 소수의 개수를 나타내는 소수 계량 함수 π(x)가 x/log x에 점근적으로 근사한다는 것을 의미한다. 이 정리는 르장드르와 가우스에 의해 처음 제안되었고, 1896년 아다마르와 드 라 발레푸생에 의해 독립적으로 증명되었다. 소수 정리의 증명에는 해석적 증명과 초등적 증명이 있으며, 해석적 증명은 리만 제타 함수와 복소해석학을 사용하고 초등적 증명은 복소해석학을 사용하지 않는다. 소수 정리와 관련된 오차 평가 및 리만 가설, 등차수열에서의 소수 정리 등 다양한 연구가 진행되었으며, 유한체 위의 기약 다항식의 분포와 유사성이 발견되었다.
더 읽어볼만한 페이지
- 해석적 수론 정리 - 천의 정리
천의 정리는 충분히 큰 짝수가 두 소수의 합 또는 소수와 반소수의 합으로 표현될 수 있다는 정수론 정리로, 골드바흐 추측에 대한 중요한 진전이며 이후 확장되었다. - 로그 - 상용로그
상용로그는 10을 밑으로 하는 로그로, 십진법에 기반하여 log x 또는 lg x로 표기되며, 지표를 통해 진수의 자릿수 파악이 용이하여 과학적 측정에 활용되고 헨리 브리그스의 공로로 '브리그스의 로그'라고도 불린다. - 로그 - 자연로그
자연로그는 밑이 e인 로그 함수로, ln(x) 등으로 표기되며 직교쌍곡선 아래 면적으로 정의되거나 지수 함수의 역함수로 정의될 수 있고, 다양한 수학적 성질과 함께 여러 분야에서 활용되며 복소 로그 함수로 확장되기도 한다. - 소수에 관한 정리 - 산술의 기본 정리
산술의 기본 정리는 1보다 큰 모든 양의 정수를 소수의 곱으로 유일하게 표현할 수 있다는 정리이다. - 소수에 관한 정리 - 페르마의 소정리
페르마의 소정리는 소수 p와 정수 a에 대해 a^p와 a가 법 p에 대해 합동이라는 정리로, p가 a의 배수가 아닐 경우 a^(p-1) ≡ 1 (mod p)로 표현되며, 소수 판별법과 RSA 암호 시스템 등에 응용된다.
2. 정의
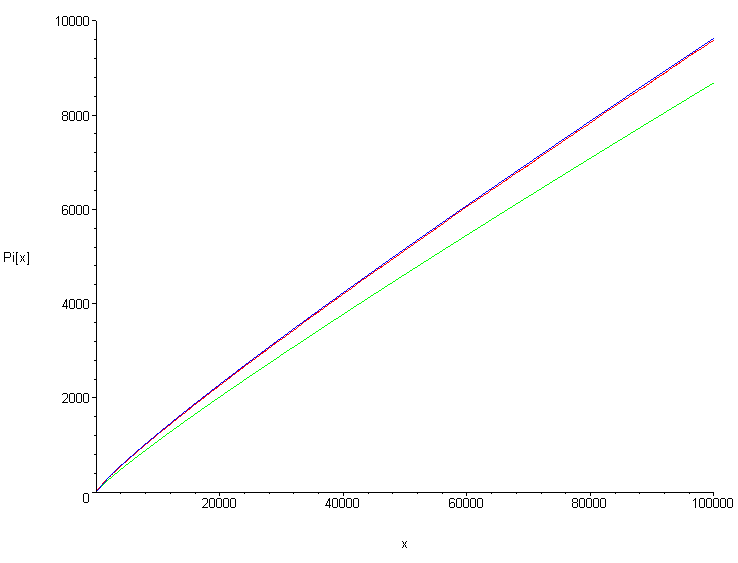
임의의 실수 에 대해 소수 계량 함수 는 보다 작거나 같은 소수의 개수를 나타내는 함수이다. 예를 들어, 10 이하의 소수는 2, 3, 5, 7로 4개이므로 이다.
소수 정리는 와 의 비가 가 무한히 커질수록 1에 수렴한다는 것을 의미한다. 즉,
:
가 성립한다. 점근 표기법에 의해 다음과 같이 표현할 수도 있다.
:
파프누티 체비쇼프는 소수 정리를 다음과 같이 개량하였다.
- 만일 어떤 상수 C에 대하여 이라면, C가 가질 수 있는 값은 1밖에 없다.
- 와 의 차이는 위아래로 4%를 벗어나지 않는다.
소수 정리는 번째 소수 이 다음을 만족한다는 진술과 동등하다.
:
점근 표기법은 다시 이 근사의 상대 오차가 이 무한대로 증가함에 따라 0에 접근한다는 의미이다. 예를 들어, 번째 소수는 이고,[4] ()log()는 로 반올림되며, 상대 오차는 약 6.4%이다.
소수 정리는 또한 다음과 동등하다.
:
여기서 와 는 각각 첫 번째 및 두 번째 체비쇼프 함수이다.
로그 적분 함수는 다음과 같이 정의된다.
:
따라서 소수 정리도 로 쓸 수 있다.
리만 가설이 참이라면, 오차 항을 다음과 같이 개선할 수 있다.
:
3. 역사
1798년 아드리앵마리 르장드르가 소수 정리를 처음 제안하였다. 카를 프리드리히 가우스도 1792년과 1793년 사이에 소수 정리를 연구했지만 발표하지는 않았다. 가우스는 1849년 자신의 회상에 따르면 "1792년 또는 1793년" 15세 또는 16세에 같은 문제를 고려했다고 한다.[6] 그는 친구 엥케에게 1849년에 단 한 번 편지로 소수 정리에 대해 언급했을 뿐이었다.[48]
1896년에는 자크 아다마르[1]와 샤를장 드 라 발레푸생[2]이 각각 독립적으로 소수 정리를 증명하였다. 두 증명 모두 복소 해석의 방법을 사용했는데, 증명의 주요 단계로서 리만 제타 함수가 s = 1 + it (t > 0) 형태의 변수 s의 모든 복소수 값에 대해 0이 아님을 보였다.[9]
1949년에는 아틀레 셀베르그[25]와 에르되시 팔[10]이 복소해석학을 사용하지 않는 소수 정리의 초등적 증명을 발표하여 수학계를 놀라게 했다. 에르되시는 이 결과를 셀베르그와 공저 논문으로 출판하려 하였으나, 셀베르그는 이를 거부하였다. 이 때문에 셀베르그와 에르되시 사이의 관계는 악화되고 말았다.[66]
셀베르그와 에르되시의 증명은 페아노 산술에서 형식화될 수 있다. 1994년, 카랄람보스 코르나로스와 코스타스 디미트라코풀로스는 그들의 증명이 IΔ₀ + exp에서 형식화될 수 있음을 증명했다.[27]
2005년, 아비가드 외 연구진은 Isabelle 정리 증명기를 사용하여 소수 정리(PNT)의 에르되시–셀베르그 증명의 컴퓨터 검증된 변형을 고안했다.[29] 2009년, 존 해리슨은 HOL Light를 사용하여 복소 해석학을 이용한 증명을 형식화했다.[30]
4. 증명
1896년 자크 아다마르와 샤를장 드 라 발레푸생이 리만 제타 함수를 이용한 복소해석학적 기법으로 소수 정리를 처음 증명하였다.[66] 이후 1949년, 복소해석학을 사용하지 않은 아틀레 셀베르그와 에르되시 팔의 초등적 증명이 발표되었다.[24][26] D. J. 뉴먼은 코시 적분 공식, 코시 적분 정리 등 복소해석학의 초등적인 기술을 사용하여 소수 정리의 간결한 증명을 제시했다.[12]
소수 정리의 증명 방법은 크게 해석적 증명과 초등적 증명으로 나눌 수 있다.
- '''해석적 증명''': 리만 제타 함수와 복소해석학적 기법을 사용한다.
- '''초등적 증명''': 아틀레 셀베르그와 에르되시 팔이 복소해석학을 사용하지 않고 증명한 방법이다.
- '''뉴먼의 증명''': D. J. 뉴먼의 증명.
4. 1. 해석적 증명의 개요
해석적 증명은 리만 제타 함수와 복소해석학적 기법을 사용한다. 수론적 함수인 소수 계량 함수의 점근적 성장은 리만 제타 함수를 통해 복소해석학적 명제로 치환할 수 있다. 우선, 다음과 같은 동치 관계는 초등적으로 보일 수 있다.[66]:
여기서
:
는 제2종 체비쇼프 함수이며, 는 폰 망골트 함수이다. 반면, 리만 제타 함수의 로그 도함수는 다음과 같이 쓸 수 있다.
:
두 합을 서로 연관짓기 위해, 다음과 같은 복소해석학적 보조정리를 사용한다.
:
따라서, 제타 함수와 체비쇼프 함수를 다음과 같이 연관지을 수 있다.
:
이제, 우변이 극한에서 1/2로 수렴함을 경로적분법으로 증명할 수 있다.[67]
4. 2. 초등적 증명의 개요
아틀레 셀베르그와 에르되시 팔은 복소해석학을 사용하지 않고 소수 정리를 증명했다. 이 증명을 '초등적 증명'이라고 부른다.[24][26]초등적 증명은 다음 점근적 등식을 이용하여 증명한다.
:
여기서 , 는 소수를 의미한다.
로 치환할 때, 다음 부등식을 유도할 수 있다.
:
소수 정리는 과 동치이다. 이 함수의 상극한을 라고 둔다면, 이 상수가 0으로 가는 것을 확인하여 소수 정리를 증명할 수 있다. 만약 이 상수가 양수라고 가정하여 모순임을 증명한다. 정의에 의해 상수 부분을 뗀 나머지 0으로 가는 함수를 다음과 같이 정의한다.
:
위 적분 형태의 부등식과 이 부등식을 이용하여 다음과 같은 유사한 형태의 부등식을 유도한다.
:
다만 이 경우 가 된다. 여기서 임을 유도하여 모순을 이끌어 낸다.[67]
4. 3. 뉴먼의 증명
D. J. 뉴먼은 코시 적분 공식, 코시 적분 정리 등 복소해석학의 초등적인 기술을 사용하여 소수 정리의 간결한 증명을 제시했다.[12]이 증명은 체비쇼프 함수 를 사용한다. 소수 정리는 과 동등하다.
함수 는 에 대한 급수에서 일부 항을 제거하여 얻으며, 은 에서 특이점을 갖지 않는다. 뉴먼의 증명에 필요한 가 유계라는 것은 체비쇼프에 의해 증명되었다.
부분 적분은 와 의 관계를 보여준다. 에 대해,
:
뉴먼의 방법은 적분
:
가 수렴함을 보여 소수 정리를 증명한다.
의 수렴을 보이기 위해, 및 로 놓는데, 여기서 이다. 그러면,
:
는 선 에서 정칙인 함수와 같다. 적분 의 수렴, 즉 소수 정리는 임을 보여 증명된다.
차이 는 코시 적분 공식을 사용하여 표현된 다음, 피적분 함수를 추정하여 가 클 때 작아짐을 보인다. 및 을 고정하여 가 영역 에서 정칙이 되도록 하고, 를 이 영역의 경계로 둔다. 코시 적분 공식은 다음을 제공한다.
:
여기서 는 뉴먼이 도입한 인자이다.
적분을 추정하기 위해 윤곽선 를 두 부분 로 나눈다. 이며, 여기서 이다. 는 유계이므로, 를 의 절댓값에 대한 상한으로 둔다.
이는 모든 에 대해 성립하므로, 이고, 소수 정리가 성립한다.
5. 등차수열에서의 소수 정리
를 보다 작은 등차수열 내의 소수의 개수로 나타낼 때, 디리클레와 르장드르는 와 가 서로소이면 다음이 성립할 것이라고 추측했고, 드 라 발레 푸생이 이를 증명했다.[31]
:
여기서 는 오일러 피 함수이다. 다시 말해, 소수는 인 모듈러 산술 모듈로 에 균등하게 분포한다. 이는 디리클레 정리보다 강력하며(각 클래스에 무한히 많은 소수가 존재한다고만 명시), 소수 정리 증명에 뉴먼(Newman)이 사용한 방법과 유사한 방법을 사용하여 증명할 수 있다.[31]
지겔-발피즈 정리는 합동류 내 소수의 분포에 대한 좋은 추정치를 제공한다.
베넷(Bennett) 외[32]는 명시적인 상수 와 를 갖는 다음 추정치를 증명했다(정리 1.3).
인 정수 와 와 서로소인 정수 가 있다고 하자. 그러면 다음이 성립하는 양의 상수 와 가 존재한다.
:
여기서
:
그리고
:
특히 다음과 같은 경우를 생각해 볼 수 있다.
:
경험적으로 3과 합동인 소수가 더 많으며, 이 "소수 경쟁"에서 거의 항상 앞서 나간다. 최초의 역전은 에서 발생한다.[33] 그러나 리틀우드는 1914년에[33] 함수 에 대해 무한히 많은 부호 변화가 있음을 보였다. 따라서 경쟁의 선두는 무한히 많은 횟수로 앞뒤로 바뀐다. 가 대부분의 시간 동안 앞서 있다는 현상을 체비쇼프 편향(Chebyshev's bias)이라고 한다. 소수 경쟁은 다른 법으로 일반화되며 많은 연구의 대상이다. 펄 투란(Pál Turán)은 와 가 와 가 와 서로소일 때 항상 자리를 바꾸는지 질문했다.[34] 앤드루 그랜빌(Andrew Granville)과 마틴은 철저한 설명과 조사를 제공한다.[33]
또 다른 예는 소수의 마지막 숫자의 분포이다. 2와 5를 제외한 모든 소수는 1, 3, 7 또는 9로 끝난다. 디리클레 정리는 점근적으로 모든 소수의 25%가 이 네 자리 숫자 각각으로 끝난다고 말한다. 그러나 경험적 증거에 따르면, 주어진 한계에 대해 1 또는 9로 끝나는 소수보다 3 또는 7로 끝나는 소수가 약간 더 많은 경향이 있다(체비쇼프 편향의 생성).[35] 이는 1과 9가 10을 법으로 한 제곱 잉여이고 3과 7이 10을 법으로 한 제곱 비잉여임을 따른다.
이 정리는 등차수열에 포함된 소수에 관해서도 확장되었으며, 이를 '''등차수열 소수 정리'''라고 한다.
즉, 등차수열 (, 와 는 서로소)에 포함된 소수 중 이하의 소수의 개수를 로 나타낼 때,
:
가 성립한다. 여기서 는 오일러의 피 함수라고 불리는 것으로, 과 서로소인 이하의 자연수의 개수를 나타낸다. 이 점근 공식은 르장드르와 디리클레에 의해 예측되었지만, 드 라 발레푸생에 의해 증명되었다. 최근, Ivan Soprounov에 의해 보다 초등적인 증명이 발견되었다.[60]
6. 오차 평가
소수 정리의 오차항은 π(''x'')와 근사 함수 (''x''/log ''x'' 또는 Li(''x'')) 사이의 차이를 나타낸다. 1901년 헬게 폰 코흐는 리만 가설이 참이면 오차 평가를 더 개선할 수 있음을 보였다.[18] 리만 가설 하에서 오차항은 다음과 같이 개선될 수 있다.
:
이 마지막 추정치는 실제로 리만 가설과 동치이다. 빅 O 표기법과 관련된 상수는 1976년 로웰 숀펠드에 의해 추정되었다.[19] (리만 가설을 가정):
:
모든 ''x'' ≥ 2657에 대해. 그는 또한 체비쇼프 소수 계량 함수 ψ(''x'')에 대한 유사한 경계를 도출했다.
:
모든 ''x'' ≥ 73.2 에 대해.
1914년에 리틀우드는 π(''x'') - li(''x'')가 무한히 자주 부호를 바꾼다는 것을 증명했다.[21] π(''x'')가 li(''x'')를 초과하는 첫 번째 ''x'' 값은 아마도 ''x'' ~ 10316 정도일 것이다. 자세한 내용은 스키위스 수를 참조.
7. 리만 함수
베른하르트 리만은 리만 함수
:
을 사용하여 π(''x'')에 관한 다음 공식을 제시했다.[64]
:
여기서 합은 제타 함수의 복소수 영점 ρ 전체를 더한 것이다.
''R''(''x'') 항만 고려하더라도, 이는 Li(''x'')보다 훨씬 더 정확한 근사값을 제공한다.
''R''(''x'')는 다음 급수를 사용하여 계산할 수 있다.[64]
:
8. 유한체 위의 기약 다항식과의 유사성
소수 정리와 유사하게 유한체 위의 기약 다항식의 분포를 설명할 수 있다. 그 형태는 고전적인 소수 정리의 경우와 매우 유사하다.
q영어를 고정된 값이라 하고, F_q영어를 q영어개의 원소를 가진 유한체라고 하자. N_n영어을 F_q영어 위에서 모닉 다항식이며 차수가 n영어인 기약 다항식의 개수라고 정의한다. 이 다항식들은 F_q영어에서 계수를 가지며 더 작은 차수의 다항식의 곱으로 표현될 수 없다. 이 설정에서 이 다항식들은 소수와 같은 역할을 한다. 왜냐하면 다른 모든 모닉 다항식은 이 기약 다항식들의 곱으로 구성되기 때문이다.
이 경우 다음이 성립한다.[47]
:
x영어 = q^n영어으로 치환하면, 우변은 다음과 같이 표현된다.
:
이는 소수 정리와의 유사성을 더 명확하게 보여준다. 차수가 n영어인 모닉 다항식(기약이 아닌 다항식 포함)은 정확히 q^n영어개이므로, 이를 다르게 표현하면, 차수가 n영어인 모닉 다항식을 무작위로 선택했을 때, 그 다항식이 기약일 확률은 약 1/n영어이다.
다음과 같이 리만 가설의 유추도 성립한다.
:
이 명제는 고전적인 경우보다 훨씬 간단하게 증명할 수 있다. 짧은 조합론적 논증을 통해 증명 가능하다.[47] F_q영어의 차수 n영어 확장의 모든 원소는 차수 d영어가 n영어을 나누는 기약 다항식의 근이다. 이러한 근을 두 가지 다른 방식으로 계산하면 다음을 얻는다.
:
여기서 합은 n영어의 모든 약수 d영어에 대한 것이다. 뫼비우스 반전을 적용하면 다음을 얻는다.
:
여기서 μ영어는 뫼비우스 함수이다. (이 공식은 가우스가 이미 알고 있었다.) 주요 항은 d=n영어일 때 발생하며, 나머지 항들의 크기를 제한하는 것은 어렵지 않다. "리만 가설" 명제는 n영어의 가장 큰 진약수가 n/2영어보다 클 수 없다는 사실에 기반한다.
9. 대한민국에서의 소수 정리 연구
대한민국의 수학계는 소수 정리와 그 응용에 대한 연구를 활발하게 진행하고 있다. 특히, 정수론 분야에서 소수 정리는 중요한 연구 주제 중 하나로 다루어진다. 대한민국의 수학자들은 소수 정리의 다양한 변형과 일반화, 그리고 소수 분포와 관련된 다른 문제들에 대한 연구를 수행하고 있다.
참조
[1]
간행물
Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques.
http://www.numdam.or[...]
Société Mathématique de France
[2]
간행물
Recherches analytiques sur la théorie des nombres premiers.
http://sciences.amis[...]
Imprimeur de l'Académie Royale de Belgique
[3]
서적
The Man Who Loved Only Numbers
https://archive.org/[...]
Hyperion Books
[4]
웹사이트
Prime Curios!: 8512677386048191063
http://primes.utm.ed[...]
University of Tennessee at Martin
2011-10-09
[5]
서적
Introduction to Analytic Number Theory
https://link.springe[...]
Springer
[6]
간행물
Werke
https://archive.org/[...]
Teubner
[7]
학술지
A Short Proof of Chebyshev's Theorem
1985-08
[8]
학술지
On Chebyshev-Type Inequalities for Primes
1982-02
[9]
서적
The Distribution of Prime Numbers
Cambridge University Press
[10]
간행물
On a new method in elementary number theory which leads to an elementary proof of the prime number theorem
https://www.renyi.hu[...]
National Academy of Sciences
1949-07-01
[11]
학술지
Simple analytic proof of the prime number theorem
[12]
학술지
Newman's short proof of the prime number theorem
http://www.maa.org/p[...]
[13]
웹사이트
254A, Notes 2: Complex-analytic multiplicative number theory
https://terrytao.wor[...]
2014-12-10
[14]
서적
Riemann's zeta function
Courier Dover Publications
[15]
간행물
Sur la fonction ζ(s) de Riemann et le nombre des nombres premiers inférieurs a une limite donnée.
https://books.google[...]
Imprimeur de l'Académie Royale de Belgique
[16]
학술지
Vinogradov's Integral and Bounds for the Riemann Zeta Function
https://faculty.math[...]
2002
[17]
학술지
Updating the error term in the prime number theorem
2016-02
[18]
학술지
Sur la distribution des nombres premiers
https://zenodo.org/r[...]
[19]
학술지
Sharper Bounds for the Chebyshev Functions ϑ(x) and ψ(x). II
[20]
학술지
Asymptotic behaviour of the variance function
[21]
간행물
Sur la distribution des nombres premiers
[22]
학술지
Contributions to the theory of the Riemann zeta-function and the theory of the distribution of primes
https://link.springe[...]
[23]
서적
Multiplicative Number Theory
Springer
[24]
서적
Number theory (New York, 2003)
Springer-Verlag
[25]
간행물
An Elementary Proof of the Prime-Number Theorem
[26]
학술지
The lord of the numbers, Atle Selberg. On his life and mathematics
https://www.ams.org/[...]
[27]
학술지
The prime number theorem and fragments of PA
http://mpla.math.uoa[...]
[28]
학술지
Dynamical generalizations of the prime number theorem and disjointness of additive and multiplicative semigroup actions
2022
[29]
학술지
A formally verified proof of the prime number theorem
[30]
학술지
Formalizing an analytic proof of the Prime Number Theorem
http://www.cl.cam.ac[...]
[31]
웹사이트
A short proof of the Prime Number Theorem for arithmetic progressions
https://citeseerx.is[...]
Cleveland State University
[32]
학술지
Explicit bounds for primes in arithmetic progressions
2018
[33]
학술지
Prime number races
http://www.dms.umont[...]
[34]
서적
Unsolved Problems in Number Theory
Springer-Verlag
[35]
학술지
Unexpected biases in the distribution of consecutive primes
2016-08-02
[36]
학위논문
Autour de la fonction qui compte le nombre de nombres premiers
https://www.unilim.f[...]
l'Université de Limoges
1998-05-26
[37]
논문
Explicit bounds for some functions of prime numbers
[38]
arXiv
Estimates of some functions over primes, without {{abbr|R.H.|Riemann hypothesis}}
2010-02-02
[39]
웹사이트
Why is pn ∼ n ln(n)?
https://math.stackex[...]
2024-10-11
[40]
논문
Sur une formule empirique de M. Pervouchine
http://gallica.bnf.f[...]
[41]
논문
La determinazione assintotica dell'nimo numero primo
[42]
논문
The n-th prime asymptotically
[43]
논문
The {{mvar|k}}th prime is greater than {{math|''k''(log ''k'' + log log ''k'' − 1)}} for {{math|''k'' ≥ 2}}
[44]
논문
New Estimates for the {{mvar|n}}th Prime Number
https://cs.uwaterloo[...]
[45]
웹사이트
Conditional Calculation of {{math|''π''(1024)}}
http://primes.utm.ed[...]
Chris K. Caldwell
2010-08-03
[46]
논문
Computing {{math|''π''(''x'')}} analytically
[47]
논문
Counting Irreducible Polynomials over Finite Fields Using the Inclusion {{pi}} Exclusion Principle
2011-12
[48]
서적
Werke(全集)
https://archive.org/[...]
Teubner
[49]
문서
ベルトランの仮説
[50]
문서
与えられた数より小さい素数の個数について
[51]
논문
Explicit bounds for some functions of prime numbers
[52]
논문
The {{mvar|k}}th prime is greater than {{math|''k''(log ''k'' + log log ''k''−1)}} for {{math|''k'' ≥ 2}}
[53]
문서
π(''x''):{{OEIS2C|id=A006880}}
[54]
문서
Difference between pi(10^n) and the integer nearest to 10^n / log(10^n).:{{OEIS2C|id=A057835}}
[55]
문서
Difference between nearest integer to Li(10^n) and pi(10^n), where Li(x) = integral of log(x) and pi(10^n) = number of primes <= 10^n:{{OEIS2C|id=A057752}}
[56]
문서
Integer nearest to 10^n / log(10^n). ''x'':{{OEIS2C|id=A057834}}
[57]
문서
Integer nearest to Li(10^n), where Li(x) = integral(0..x, dt/log(t)).:{{OEIS2C|id=A057754}}
[58]
웹사이트
Conditional Calculation of pi(10{{sup|24}})
http://primes.utm.ed[...]
Chris K. Caldwell
2010-08-03
[59]
웹사이트
Computing π(x) Analytically)
https://arxiv.org/ab[...]
2012-07-25
[60]
웹사이트
A short proof of the Prime Number Theorem for arithmetic progressions
http://academic.csuo[...]
Cleveland State University
2022-08-07
[61]
논문
Vinogradov's Integral and Bounds for the Riemann Zeta Function
https://faculty.math[...]
2002
[62]
논문
Sur la distribution des nombres premiers
https://zenodo.org/r[...]
[63]
논문
Sur la distribution des nombres premiers
[64]
MathWorld
Gram Series
[65]
논문
Counting Irreducible Polynomials over Finite Fields Using the Inclusion-Exclusion Principle
http://www.jstor.org[...]
2011-12
[66]
저널
[67]
서적
[68]
저널
On Selberg's elementary proof of the prime number theorem
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

